Question

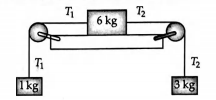
Three masses of $1\, kg , 6\, kg$ and $3\, kg$ are connected to each other with strings and are placed on a table as shown in figure. What is the acceleration with which the system is moving? (Take $g=10\, m\, s ^{-2}$ )

• A. $zero$
• B. $1\, m\, s ^{-2}$
• C. $2\, m\, s ^{-2}$
• D. $3\, m\, s ^{-2}$

Answer 1

Answer: (C)

Here, $m_{1}=1 kg , m_{2}=6 kg$ and $m_{3}=3 kg$
Let $a$ be the acceleration with which the system is moving. The equations of motion of three masses are
$m_{1} a=T_{1}-m_{1} g $
$m_{2} a=T_{2}-T_{1} $
$m_{3} a=m_{3} g-T_{2}$
Adding $(i), (ii) $ and $(iii)$, we get
$a\left(m_{1}+m_{2}+m_{2}\right)=\left(m_{3}-m_{1}\right) g $
$\therefore a=\frac{\left(m_{3}-m_{1}\right) g}{\left(m_{1}+m_{2}+m_{3}\right)}=\frac{(3-1) \times 10}{1+6+3}=2 m s ^{-2}$