Q.
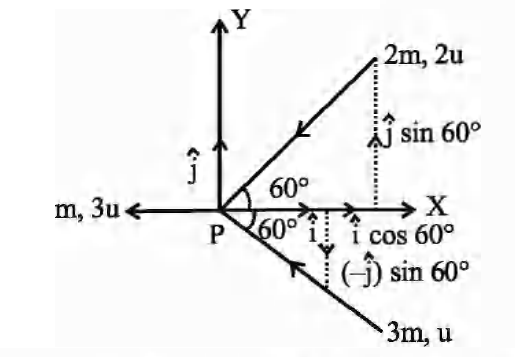
Three masses $m, 2m$ and $3m$ are moving in x-y plane with speed $3u, 2u$ and $u$ respectively as shown in figure. The three masses collide at the same point at $P$ and stick together. The velocity of resulting mass will be :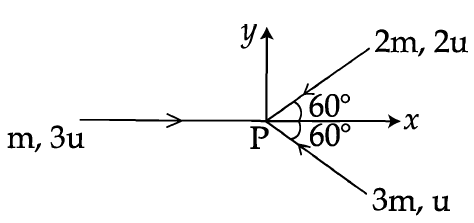
Solution:
From the law of conservation of momentum we know that,
$m_1u_1 + m_2u_2 +\,.... = m_1v_1 +m_2v_2\, +....$
Given $m_1 = m,m_2 = 2m$ and $m_3 = 3m$ and $U_1 = 3u, u_2 = 2u$ and $u_3 = u$
Let the velocity when they stick $=\vec{v}$
Then, according to question.
$m\times3u\left(\hat{i}\right)+2m\times 2u\left(-\hat{i}\,cos\,60^{°}-\hat{j}\,sin\,60^{°}\right)$
$+ 3m\times u\left(-\hat{i}\,cos\,60^{°}+\hat{j}\,sin\,60^{°}\right)$
$=\left(m+2m+3m\right)\vec{v}$
$\Rightarrow 3mu\hat{i}-4mu \frac{\hat{i}}{2}-4mu\left(\frac{\sqrt{3}}{2}\hat{j}\right)-3mu \frac{\hat{i}}{2}+3mu\left(\frac{\sqrt{3}}{2}\hat{j}\right)=6m\,\vec{v}$
$\Rightarrow mu\hat{i}-\frac{3}{2}mu\hat{i}-\frac{\sqrt{3}}{2}mu\hat{j}=6m\,\vec{v}$
$\Rightarrow \vec{v}$$\frac{u}{12}\left(-\hat{i}-\sqrt{3\hat{j}}\right)$From the law of conservation of momentum we know that,
$m_1u_1 + m_2u_2 +\,.... = m_1v_1 +m_2v_2\, +....$
Given $m_1 = m,m_2 = 2m$ and $m_3 = 3m$ and $U_1 = 3u, u_2 = 2u$ and $u_3 = u$
Let the velocity when they stick $=\vec{v}$
Then, according to question.
$m\times3u\left(\hat{i}\right)+2m\times 2u\left(-\hat{i}\,cos\,60^{°}-\hat{j}\,sin\,60^{°}\right)$
$+ 3m\times u\left(-\hat{i}\,cos\,60^{°}+\hat{j}\,sin\,60^{°}\right)$
$=\left(m+2m+3m\right)\vec{v}$
$\Rightarrow 3mu\hat{i}-4mu \frac{\hat{i}}{2}-4mu\left(\frac{\sqrt{3}}{2}\hat{j}\right)-3mu \frac{\hat{i}}{2}+3mu\left(\frac{\sqrt{3}}{2}\hat{j}\right)=6m\,\vec{v}$
$\Rightarrow mu\hat{i}-\frac{3}{2}mu\hat{i}-\frac{\sqrt{3}}{2}mu\hat{j}=6m\,\vec{v}$
$\Rightarrow \vec{v}$$\frac{u}{12}\left(-\hat{i}-\sqrt{3\hat{j}}\right)$