Question

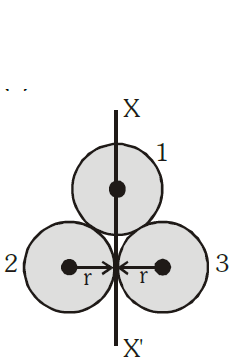
Three identical spherical shells, each of mass $m$ and radius $r$ are placed as shown in figure. Consider an axis $X X' $ which is touching to two shells and passing through diameter of third shell. Moment of inertia of the system consisting of these three spherical shells about $XX' $ axis is

• A. $ \frac{16}{5} mr^2 $
• B. $ 4 m r^2 $
• C. $ \frac{11}{5} mr^2 $
• D. $ 3mr^2 $

Answer 1

Answer: (B)

Net moment of inertia of the system,
$ I = I_1 + I_2 + I_3 $
The moment of inertia of a shell about its diameter,
$ I_1 = \frac{2}{3} mr^2 $
The moment of inertia of a shell about its tangent is given by
$ I_2 = I_3 = I_1 + mr^2 = \frac{2}{3} mr^2 + mr^2 = \frac{5}{3} mr^2 $
$ \therefore I = 2 \times \frac{5}{3} mr^2 + \frac{2}{3} mr^2 = \frac{12mr^2}{3} = 4mr^2 $