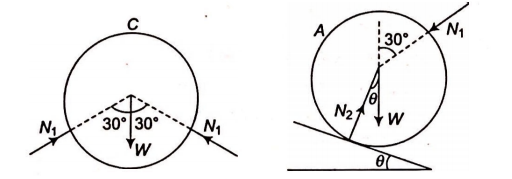
Q.
Three identical rigid circular cylinders $A, B$ and $C$ are arranged on smooth inclined surfaces as shown in figure The least value of $\theta$ that prevent the arrangement from collapse is
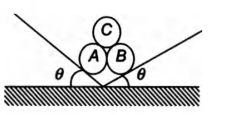
Laws of Motion
Solution: