Q.
Three identical charges, each $2 \,\mu \,C$ lie at the vertices of a right angled triangle as shown in the figure. Forces on the charge at $B$ due to the charges at $A$ and $C$ respectively are $F_{1}$ and $F_{2} .$ The angle belween their resultanl force and $F_{2}$ is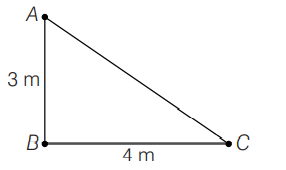
AP EAMCETAP EAMCET 2016
Solution:
