Question

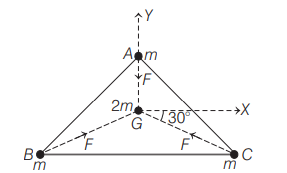
Three equal masses of $m \,kg$ each are fixed at the vertices of an equilateral triangle $A B C^{\prime}$ and a mass $2 \,m$ is placed at centroid $G$ of the triangle as shown below.

The force acting on a mass $2 \,m$ placed at the centroid $G$ of the triangle is

• A. $\frac{2 G m^{2}}{\sqrt{2}}$
• B. $2 G m^{2}$
• C. $6 G m^{2}$
• D. zero

Answer 1

Answer: (D)

The angle between $G C$ and positive $X$-axis is $30^{\circ}$ and so is the angle between $G B$ and negative $X$-axis.

From figure, resolving the forces on $2 m$ due to masses at $B$ and $C$ along $X$-axis.
$\Rightarrow \left| F _{x \text { (net) }}\right|=\left|F \cos 30^{\circ} \hat{ i }-F \cos 30^{\circ} \hat{ i }\right|=0$
Similarly along $Y$-axis,
$\left| F _{y \text { (net) })}\right| =\left|F \hat{ j }-\left(F \sin 30^{\circ}+F \sin 30^{\circ}\right) \hat{ j }\right| $
$=\left|F \hat{ j }-\left(\frac{F}{2}+\frac{F}{2}\right) \hat{ j }\right|=|F \hat{ j }-F \hat{ j }|=0$
$F_{\text {net }}=$ Resultant force on mass at $G$ due to masses at $A, B$ and $ C=\sqrt{F_{x \text { (net) }}^{2}+F_{y \text { (net) }}^{2}}=0$