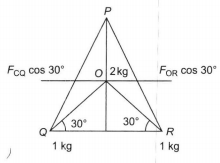
Q. Three equal masses of $1\, kg$ each are placed at the vertices of an equilateral triangle $PQR$ and a mass of $2\, kg$ is placed at the centroid O of the triangle which is at a distance of $\sqrt{2} m$ from each of the vertices of the triangle. The force, in newton, acting on the mass of $2\, kg$ is
Motion in a Plane
Solution:
Given, $OP =OQ =OR =\sqrt{2} \, m$
The gravitational force on the mass $2\, kg$ due to the $1\, kg$ mass at $P$ is $F_{OP} = G \frac{2 \times 1}{(\sqrt2)^2} = G$ along $OP$
Similarly, $F_{OQ} = G_1 \frac{2 \times 1}{(\sqrt2)^2} = G_1$ along $OQ$ and
$F_{OR} = G_1 \frac{2 \times 1}{(\sqrt2)^2} = G_1$ along $OR$
$F_{OQ} \cos 30^{\circ}$ and $F_{OR} \cos 30^{\circ}$ are equal and acting in opposite directions, thus they cancel out. Hence, the resultant force on the $2\, kg$ mass at $O$, is
$F = F_{OP} - (F_{OQ} \sin \, 30^{\circ} + F_{OR} \sin \, 30^{\circ})$
$=G_1 - \left(\frac{G_1}{2} + \frac{G_1}{2}\right)$
$= 0$