Q.
Three elastic wires, $PQ$, $PR$ and $PS$ support a body $P $ of mass $M$, as shown in figure. The wires are of the same material and cross-sectional area, the middle one being vertical. The load carried by middle wire is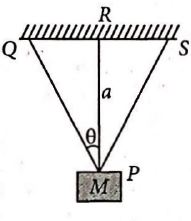
Mechanical Properties of Solids
Solution:
