Question

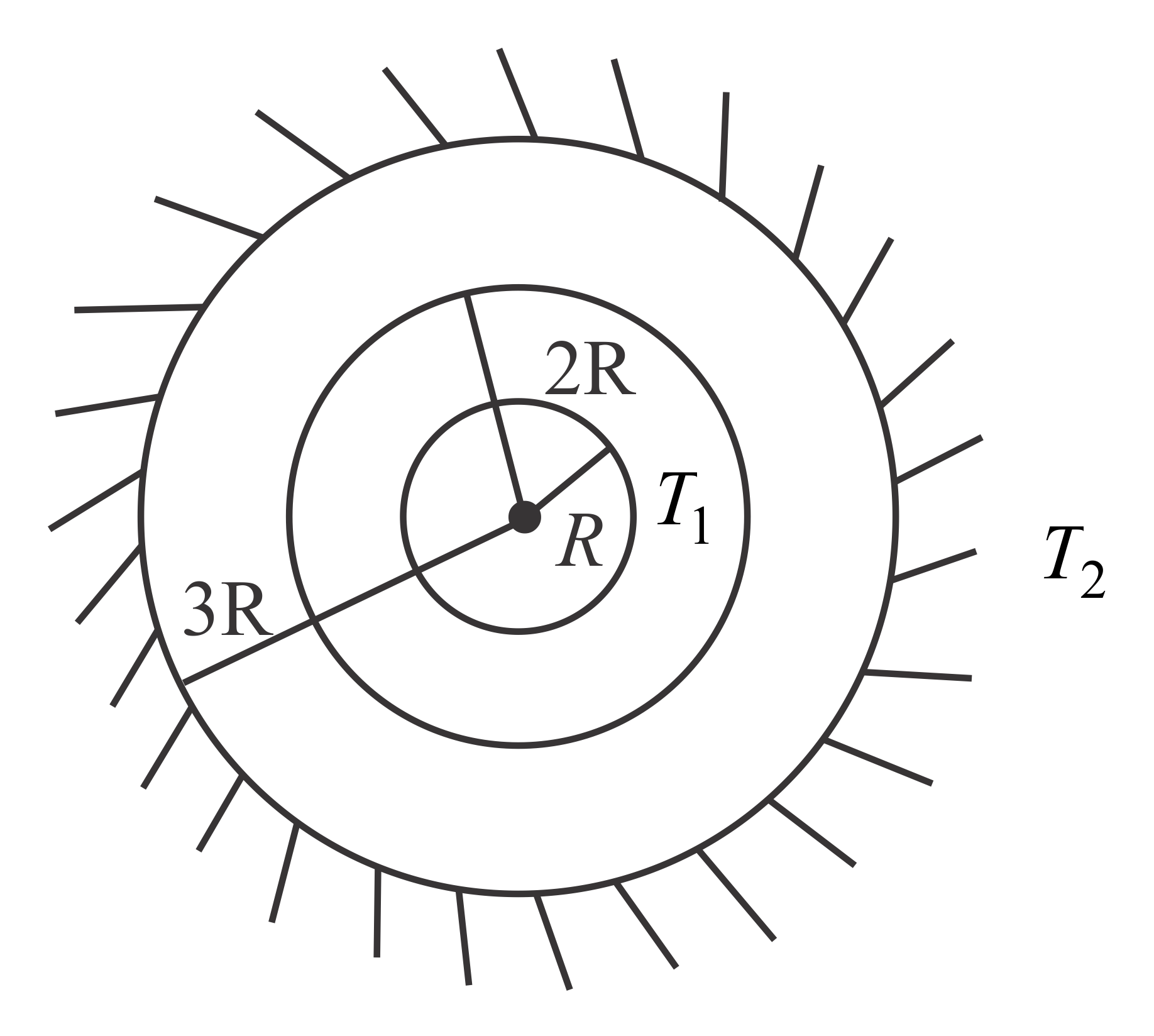
Three concentric thin spherical shells are shown in figure. Outermost sphere can't radiate in outer space. The innermost and the outermost shells are maintained at $T_{1}K$ and $T_{2}K$ respectively. Assume that the three shells behave as black body. The steady state temperature of the middle shell is $\left(\frac{T_{1}^{4}}{x} + \frac{T_{2}^{4}}{y}\right)^{\frac{1}{4}}$ . Value of $x+4y$ is

Answer 1

Let $T_{i}=$ steady-state temperature of the middle shell.
and $T_{1}>T_{2}$
In steady-state condition, the heat radiation transfer between the outermost shell and middle shell will be equal to the heat radiation transfer between the innermost shell and middle shell.
From Stefan's law of radiation,
$\sigma 4 \pi R^{2} T_{1}^{4}-T_{ i }^{4}=\sigma 4 \pi 2 R^{2} T_{ i }^{4}-T_{2}^{4} T_{1}^{4}-T_{ i }^{4}=4 T_{ i }^{4}-T_{2}^{4}$
$\Rightarrow T_{ i }^{4}=\frac{T_{1}^{4}+4 T_{2}^{4}}{5} $
$\Rightarrow T_{ i }=\frac{T_{1}^{4}}{5}+\frac{T_{2}^{4}{ }^{\frac{1}{4}}}{\frac{5}{4}} $
$\Rightarrow x+y=10$