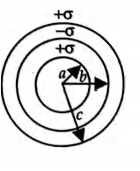
Question

Three concentric charged metallic spherical shells $A, B$ and $C$ have radii $a, b$ and $c ;$ charge densities $\sigma,-\sigma$ and $\sigma$ and potentials $V_{A}, V_{B}$ and $V_{C}$ respectively. Then which of the following relations is correct?

• A. $V_{A}=(a+b+c) \frac{\sigma}{\varepsilon_{0}}$
• B. $V_{B}=\left(\frac{a^{2}}{b}-b+c\right) \frac{\sigma}{\varepsilon_{0}}$
• C. $V_{C}=\left(\frac{a^{2}+b^{2}}{c}+c\right) \frac{\sigma}{\varepsilon_{0}}$
• D. $V_{A}=V_{B}=V_{C}=(a+b+c) \frac{\sigma}{\varepsilon_{0}}$

Answer 1

Answer: (B)

Potential due to charged shell at an outside point
$ = \frac{1}{4\pi \varepsilon_0} \frac{q}{r}$
where $r$ is the distance of point from the centre of the shell while that inside the shell $ = \frac{1}{4\pi \varepsilon_0} \frac{q}{R}$
where $R$ is the radius of the shell
Charges on the three shells are given by
$q_A = 4 \pi a^2 \sigma$,
$q_B = -4\pi b^2 \sigma$,
$ q_c = 4\pi c^2 \sigma$
$\therefore V_A = \frac{1}{4 \pi \varepsilon_0} \left[ \frac{q_A}{a} + \frac{q_B}{b} + \frac{q_C}{c} \right]$
$ = \frac{1}{4\pi \varepsilon_0} \left[ \frac{4 \pi a^2 \sigma}{a} - \frac{4 \pi b^2 \sigma}{b} + \frac{4 \pi c^2 \sigma}{c} \right] = \frac{\sigma}{\varepsilon_0} (a - b + c)$
$V_B = \frac{1}{4\pi \varepsilon_0}\left[\frac{q_A}{b} + \frac{q_B}{b} +\frac{ q_C}{c}\right]$
$= \frac{1}{4 \pi \varepsilon_0} \left[\frac{4\pi a^2 \sigma}{b} - \frac{4\pi b^2 \sigma}{b} + \frac{4 \pi c^2 \sigma}{c} \right]$
$=\frac{4 \pi \sigma}{4 \pi \varepsilon_{0}}\left[\frac{a^{2}}{b}-b+c\right]=\frac{\sigma}{\varepsilon_{0}}\left(\frac{a^{2}}{b}-b+c\right) $
$ V_{C} =\frac{1}{4 \pi \varepsilon_{0}}\left[\frac{q_{A}}{c}+\frac{q_{B}}{c}+\frac{q_{C}}{c}\right] $
$=\frac{1}{4 \pi \varepsilon_{0}}\left[\frac{4 \pi a^{2} \sigma}{c}-\frac{4 \pi b^{2} \sigma}{c}+\frac{4 \pi c^{2} \sigma}{c}\right]$
$=\frac{\sigma}{\varepsilon_{0}}\left(\frac{a^{2}-b^{2}}{c}+c\right) $