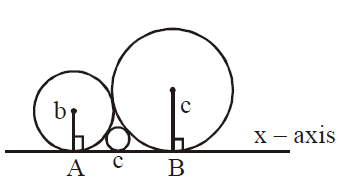
Q. Three circles of radii $a, b, c(a < b < c)$touch each other externally. If they have x-axis as a common tangent, then :
Solution:
$AB =AC +CB $
$ \sqrt{\left(b+c\right)^{2} -\left(b-c\right)^{2}} $
$ = \sqrt{\left(b+a\right)^{2} -\left(b-a\right)^{2} } + \sqrt{\left(a+c\right)^{2}-\left(a-c\right)^{2}} $
$ \sqrt{bc} = \sqrt{ab} + \sqrt{ac} $
$ \frac{1}{\sqrt{a}} = \frac{1}{\sqrt{c}} + \frac{1}{\sqrt{b}} $