Question

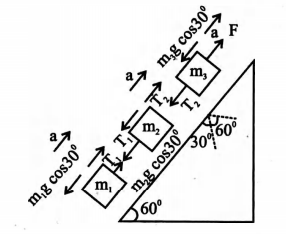
Three blocks of mass $m_{1}=2.0, m_{2}=4.0$ and $m_{3}=6.0$ $kg$ are connected by strings on a frictionless inclined plane of $60^{\circ},$ as shown in the figure. $A$ force $F=120$ $N$ is applied upward along the incline to the uppermost block, causing an upward movement of the blocks. The connecting cords are light. The values of tension $T _{1}$ and $T$, in the cords are

• A. $T_{1}=20 N , T _{2}=60 N$
• B. $T_{1}=60 N , T _{2}=60 N$
• C. $T_{1}=30 N , T _{2}=50 N$
• D. $T_{1}=20 N , T _{2}=100 N$

Answer 1

Answer: (A)

The free body diagram are given below:

For the motion of mass $m_{1}, m_{2}$ and $m_{3},$ we have
$T _{1}- m _{1} g \cos 30^{\circ}= m _{1} a \ldots$ (i)
$T _{2}- T _{1}- m _{2} g \cos 30^{\circ}= m _{2} a \ldots$ (ii)
$F - T _{2}- m _{3} g \cos 30^{\circ}= m _{3} a \ldots$ (ii)
Adding Eqs., (i), (ii) and (iii), we get
$F=\left(m_{1}+m_{2}+m_{3}\right) g \cos 30^{\circ}=\left(m_{1}+m_{2}+m_{3}\right) a$
$\Rightarrow \frac{F}{m_{1}+m_{2}+m_{3}}=g \cos 30^{\circ}=a$
$ \Rightarrow \frac{120}{12} -10 \times \frac{\sqrt{3}}{2}=a$
$ \Rightarrow a=10\left(1-\frac{\sqrt{3}}{2}\right) $
Now, $T_{1} =m_{1}\left(a+g \cos 30^{\circ}\right) $
$=2\left(10-\frac{10 \sqrt{3}}{2}+10 \frac{\sqrt{3}}{2}\right)=20 N $
$T_{2} =a\left(m_{1}+m_{2}\right)+\left(m_{1}+m_{2}\right) g \cos 30^{\circ} $
$=6 \times 10 =60 N $