Q.
Three blocks are connected by massless strings on a frictionless inclined plane of $30^{\circ}$ as shown in the figure. A force of $104\, N$ is applied upward along the incline to mass $m_{3}$ causing an upward motion of the blocks. What is the acceleration of the blocks? (Assume, acceleration due to gravity, $\left.g=10\, m / s ^{2}\right)$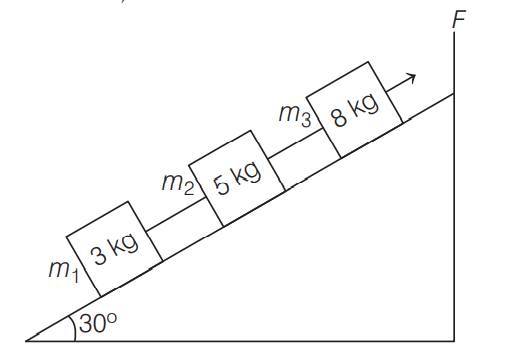
TS EAMCET 2019
Solution:
