Question

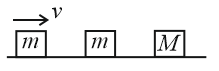
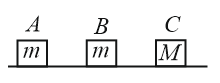
Three blocks $A, \, B$ and $C$ are lying on a smooth horizontal surface, as shown in the figure. $A$ and $B$ have equal masses $m$ while $C$ has mass $M$ . Block $A$ is given an initial speed $v$ towards $B$ due to which it collides with $B$ perfectly inelastically. The combined mass collides with $C$ , also perfectly inelastically. $\frac{5}{6}\text{t}\text{h}$ of the initial kinetic energy is lost in the whole process. What is the value of $M / m$ ?

• A. $3$
• B. $4$
• C. $5$
• D. $2$

Answer 1

Answer: (B)

$mv=\left(m + m\right)v^{′}$
$\left(m + m\right)v^{′}=\left(m + m + M\right)v_{f}$
$\therefore $ final velocity $v_{f}=\frac{m}{2 m + M}v$
Initial energy $=\frac{1}{2}mv^{2}$
Final energy $ \, =\frac{1}{2}\left(2 m + M\right)\left(\frac{m v}{2 m + M}\right)^{2}$
Given that $\frac{5}{6}\frac{1}{2}mv^{2}=\frac{1}{2}mv^{2}-\frac{1}{2}\left(2 m + M\right)\left(\frac{m v}{2 m + M}\right)^{2}$
$\frac{1}{12}mv^{2}=\frac{1}{2}\frac{m^{2} v^{2}}{\left(2 m + M\right)}$
$6m=2m+M$
$\frac{M}{m}=4$