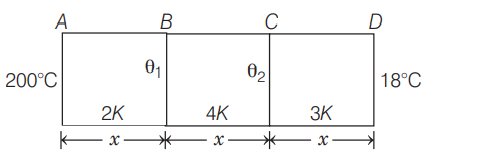
Question

Three bars of equal lengths and equal area of cross-sections are connected in series. Their thermal conductivities are in the ratio of $2: 4: 3$. If the open ends of the first and the last bars are at temperature $200^{\circ} C$ and $18^{\circ} C$, respectively in the steady state, then calculate the temperatures of both the junctions.

• A. $116^{\circ} C , 74^{\circ} C$
• B. $120^{\circ} C , 180^{\circ} C$
• C. $125^{\circ} C , 50^{\circ} C$
• D. $130^{\circ} C , 40^{\circ} C$

Answer 1

Answer: (A)

Suppose $\theta_{1}$ and $\theta_{2}$ be the temperatures of junctions $B$ and $C$, respectively.

In the steady state, the rate of flow of heat through each bar will be same.
$\frac{Q}{t}=\frac{2 K \times A\left(200-\theta_{1}\right)}{x}=\frac{4 K \times A\left(\theta_{1}-\theta_{2}\right)}{x} $
$=\frac{3 K \times A\left(\theta_{2}-18\right)}{x} $
$2\left(200-\theta_{1}\right)=4\left(\theta_{1}-\theta_{2}\right)=3\left(\theta_{2}-18\right) $
$200-\theta_{1}=2 \theta_{1}-2 \theta_{2} $
and $ 4 \theta_{1}-4 \theta_{2}=3 \theta_{2}-54 $
$\Rightarrow 3 \theta_{1}-2 \theta_{2}=200$
and $ 4 \theta_{1}-7 \theta_{2}=-54 $
Solving the given expressions for $\theta_{1} $ and $ \theta_{2},$ we get
$\Rightarrow \theta_{2}=74^{\circ} C$
$ \theta_{1}=116^{\circ} C$