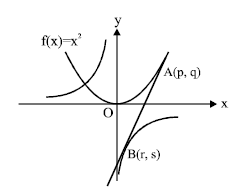
Question

There is a point $(p, q)$ on the graph of $f(x)=x^{2}$ and a point $(r, s)$ on the graph of $g(x)=\frac{-8}{x}$, where $p>$ 0 and $r>0$. If the line through $(p, q)$ and $(r, s)$ is also tangent to both the curves at these points, respectively, then the value of $p + r$ is

Answer 1

$y=x^{2}$ and $y=-\frac{8}{x} ; q=p^{2}$ and $s=\frac{8}{r}\,\,\, ...(i)$
Equation $\frac{d y}{d x}$ at $A$ and $B$, we get
$2 p =\frac{8}{ r ^{2}} \,\,\, ...(ii)$
$\Rightarrow pr ^{2}=4$

Now $m _{A B }=\frac{ q - s }{ q - r } $
$\Rightarrow 2 p =\frac{ p ^{2}+\frac{8}{ r }}{ p - r }$
$\Rightarrow p ^{2}=2 pr +\frac{8}{ r } $
$\Rightarrow p ^{2}=\frac{16}{ r }$
$\Rightarrow \frac{16}{ r ^{4}}=\frac{16}{ r }$
$\Rightarrow r =1( r \neq 0) $
$\Rightarrow p =4$
$\therefore r =1, p =1$
Hence $p + r =5$