Q.
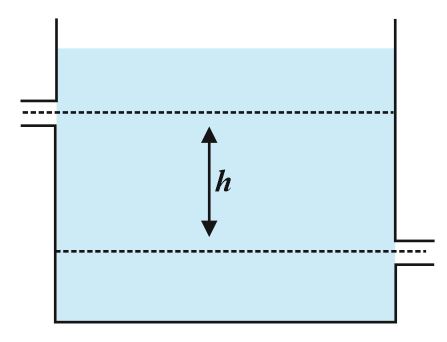
There are two identical small holes of area of cross-section $\textit{A}$ on the opposite sides of a tank containing a liquid of density $\rho $ . The difference in height between the holes is $\textit{h}$ . Tank is resting on a smooth horizontal surface, horizontal force which has to be applied on the tank to keep it in equilibrium is
NTA AbhyasNTA Abhyas 2020
Solution:
