1. Tardigrade
  2. Question
  3. Physics
  4. The Young's modulus of steel is twice that of brass. Two wires of same length and of same area of cross section, one of steel and another of brass are suspended from the same roof. If we want the lower ends of the wires to be at the same level, then the weights added to the steel and brass wires must be in the ratio of

Question Error Report

Thank you for reporting, we will resolve it shortly

Back to Question

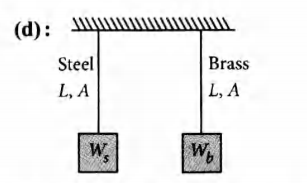
Q. The Young's modulus of steel is twice that of brass. Two wires of same length and of same area of cross section, one of steel and another of brass are suspended from the same roof. If we want the lower ends of the wires to be at the same level, then the weights added to the steel and brass wires must be in the ratio of

AIPMTAIPMT 2015Mechanical Properties of Solids

Solution:

Let $L$ and A be length and area of cross section of each wire.
In order to have the lower ends of the wires to be at the same level (i.e. same elongation is produced in both wires), let weights $ W_s$, and $W_b $
are added to steel and brass wires respectively.
Then By definition of Young's modulus, the elongation produced in the steel wire is
$ \Delta L_s = \frac{ W_s L}{ Y_s A}$ (as $Y+ \frac{W/A}{\Delta L/L}$)
and that in the brass wire is
$ \Delta L_b = \frac{ W_b L}{ Y_b A}$
But $ \Delta L_s = \Delta L_b$ (given)
$\therefore \frac{W_sL}{Y_s A}= \frac{W_b L}{ Y_b A }$
or $\frac{W_s}{W_b} =\frac{Y_s}{Y_b} $
As $ \frac{Y_s}{Y_b} = 2$ (given)
$ \frac{W_s}{W_b} = \frac{2}{1}$

Solution Image