Question

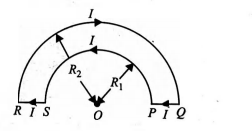
The wire loop $PQRS$ formed by joining two semi circular wires of radii $R_{1}$ and $R_{2}$ carries a current $I$ as shown the figure. The magnitude of magnetic induction at the centre $O$ is

• A. $\frac{\mu_{0} I}{4}\left(\frac{1}{R_{2}}-\frac{1}{R_{1}}\right)$
• B. $\frac{\mu_{0} I}{4}\left(\frac{1}{R_{1}}-\frac{1}{R_{2}}\right)$
• C. $\mu_{0} I\left(\frac{1}{R_{2}}-\frac{1}{R_{1}}\right)$
• D. $\mu_{0} I\left(\frac{1}{R_{1}}-\frac{1}{R_{2}}\right)$

Answer 1

Answer: (B)

The magnetic induction at $O$ due to current through $Q P$ and $S R$ will be zero.
Thus, the magnetic induction at $O$ will be only due to current through semicircles of radii $R_{1}$ and $R_{2}$ respectively.
Magnetic field at $O$ due to semicircular arc $P S$ of radius $R_{1}$ will be
$B_{1}=\frac{\mu_{0}}{4 \pi} \frac{\pi I}{R_{1}}$.
Its direction is perpendicular to coil directed outwards. Magnetic field at $O$ due to semicircular arc $R Q$ of radius $R_{2}$ will be,
$B_{2}=\frac{\mu_{0}}{4 \pi} \frac{\pi I}{R_{2}}$.
Its direction is perpendicular to coil directed inwards.
The resultant magnetic field at $O$, $\vec{B}=\left(B_{1}-B_{2}\right)$ outwards
$\therefore B=\frac{\mu_{0}}{4 \pi} I \pi\left[\frac{1}{R_{1}}-\frac{1}{R_{2}}\right]=\frac{\mu_{0}}{4} I\left[\frac{1}{R_{1}}-\frac{1}{R_{2}}\right]$