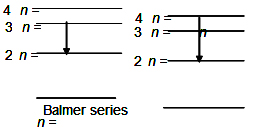Question

The wavelength of the first spectral line in the Balmer series of the hydrogen atom is $6561 \, \overset{^\circ }{A}$ . The wavelength of the second spectral line in the Balmer series of singly ionized helium atom is

• A. $1215\overset{^\circ }{A}$
• B. $1640\overset{^\circ }{A}$
• C. $2430\overset{^\circ }{A}$
• D. $4687\overset{^\circ }{A}$

Answer 1

Answer: (A)

For hydrogen or hydrogen type atoms
$\frac{1}{\lambda }=\left(R Z\right)^{2}\left(\frac{1}{n_{f}^{2}} - \frac{1}{n_{i}^{2}}\right)$
In the transition from $n_{i} \rightarrow \, n_{f}$
$\therefore \, \lambda \, \propto \, \frac{1}{Z^{2} \left(\frac{1}{n_{f}^{2}} - \frac{1}{n_{i}^{2}}\right)}$
$\therefore \quad \frac{\lambda_2}{\lambda_1}=\frac{Z_1^2\left(\frac{1}{n_f^2}-\frac{1}{n_i^2}\right)_1}{Z_2^2\left(\frac{1}{n_f^2}-\frac{1}{n_i^2}\right)_2}$
$\lambda_2=\frac{\lambda_1 Z_1^2\left(\frac{1}{n_f^2}-\frac{1}{n_i^2}\right)_1}{Z_2^2\left(\frac{1}{n_f^2}-\frac{1}{n_i^2}\right)_2}$
Substituting the values, we have
$ \, \, =\frac{\left(\right. 6561 \left.\right) \left(1\right)^{2} \left(\frac{1}{2^{2}} - \frac{1}{3^{2}}\right)}{\left(2\right)^{2} \left(\frac{1}{2^{2}} \, - \, \frac{1}{4^{2}}\right)}$ $=1215\overset{^\circ }{A}$