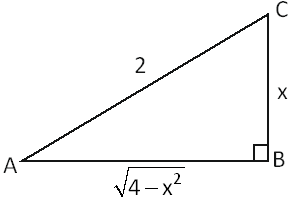
Question

The volume of the greatest cone obtained by rotating a right-angled triangle of hypotenuse $2$ units about a side is $\frac{k \pi }{9 \sqrt{3}}$ cubic units, then the value of $k$ is equal to

Answer 1

The volume generated $=V=\frac{1}{3}\pi r^{2}h$
$=\frac{1}{3}\pi \left(4 - x^{2}\right)\left(x\right)$
For maximum volume, $\frac{d V}{d x}=0$
$\Rightarrow 4-3x^{2}=0\Rightarrow x=\frac{2}{\sqrt{3}}$
$V_{m a x}=\frac{\pi }{3}\left(4 - \frac{4}{3}\right)\frac{2}{\sqrt{3}}$ $=\frac{16 \pi }{9 \sqrt{3}}$
Also, $\frac{d^{2} V}{d x^{2}} < 0$