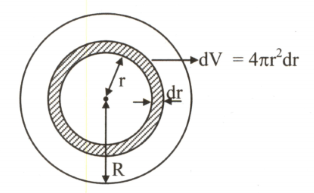
Question

The volume charge density of a sphere carrying charge $Q$ and of radius $R$ is proportional to the square of the distance from the centre. The ratio of the magnitude of the electric field at a distance $2R$ from the centre to that at a distance of $\frac{R}{2}$ from the centre is

Answer 1

As given,
$\rho =Cr^{2}$ [where $\rho =$ volume charge density]
$q\left(\right.r\left.\right)= \int \limits_{0}^{r}\left(4 \pi r^{2} dr\right)\rho $
$=\int\limits _{0}^{r}4\pi r^{2}\cdot Cr^{2}dr=\frac{4}{5}\pi Cr^{5}$
$\left(\text{E} \left|\right.\right)_{r = 2 \text{R}}=\frac{\left(\text{kq}\right)_{\left(\right. 2 \text{R} \left.\right)}}{\left(\right. 2 \text{R} \left.\right)^{2}}=\frac{\text{k} \left(\right. \frac{4}{5} \left.\right) \pi \left(\text{CR}\right)^{5}}{4 \left(\text{R}\right)^{2}}$
..... $\left[\right.\because $ sphere has radius $R;$ so $r\leq R$ for enclosed charge]
$=\frac{k \pi CR^{3}}{5}$
$\left(\text{E} \left|\right.\right)_{r = \text{R} / 2}=\frac{\left(\text{kq}\right)_{\left(\right. \text{R} / 2 \left.\right)}}{\left(\right. \frac{\text{R}}{2} \left.\right)^{2}}=\frac{\text{k} \left(\right. \frac{4}{5} \left.\right) \pi \text{C} \left(\right. \frac{\text{R}}{2} \left.\right)^{5}}{\left(\right. \frac{\text{R}}{2} \left.\right)^{2}}=\frac{\text{k} \pi \left(\text{CR}\right)^{3}}{5 \times 2}$
$\Rightarrow \frac{E_{\left(\right. 2 R \left.\right)}}{E_{\left(\right. R / 2 \left.\right)}}=2$