Q.
The voltage time $(V-t)$ graph for triangular wave having peak value $V_{0}$ is as shown in the figure. The rms value of $V$ in time interval from $t=0$ to $T / 4$ is $\frac{V_{0}}{\sqrt{n}}$. Find $n$.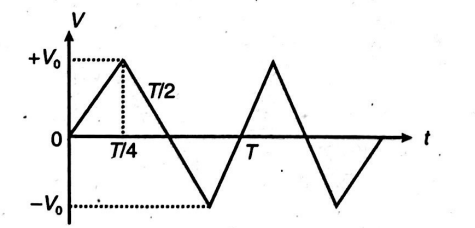
Alternating Current
Solution: