Q.
The velocity-time graphs of a car and a scooter are shown in the figure.
(i) The difference between the distance travelled by the car and the scooter in $15\, s$ and
(ii) the time at which the car will catch up with the scooter are, respectively.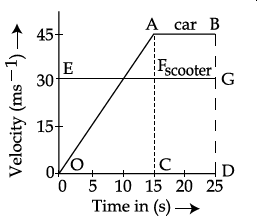
Solution: