Q.
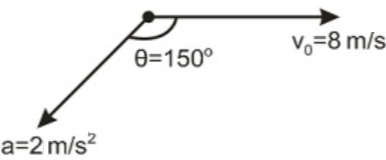
The velocity and acceleration of a point-like body at the initial moment of its motion are $v_{0 \, }=8 \, m \, s^{- 1}$ and $a=2 \, m \, s^{- 2}$ respectively. The acceleration vector of the body remains constant. The minimum radius of curvature of the trajectory of the body is
NTA AbhyasNTA Abhyas 2020Laws of Motion
Solution:
