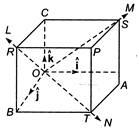
Q. The vectors of magnitude $a, 2a, 3a $ meet at a point and their directions are along the diagonals of three adjacent faces of a cube. Then, the magnitude of their resultant is
Solution:
Suppose that the sides of cube are unity and unit vector along OA, OB and OC are $ \hat{i},\text{ }\hat{j},\text{ }\hat{k} $ respectively. OR, OS, OT are diagonals of cube having corresponding vector a, 2a and 3a (Magnitude) respectively.
$ \therefore $ Unit vector along $ OR=\frac{\hat{j}+\hat{k}}{\sqrt{2}} $
$ \therefore $ Vector along $ \overrightarrow{OR}=a\left( \frac{\hat{j}+\hat{k}}{\sqrt{2}} \right) $ Similarly, vector along $ \overrightarrow{OS}=2a\left( \frac{\hat{k}+\hat{i}}{\sqrt{2}} \right) $ and vector along $ \overrightarrow{OT}=3a\left( \frac{\hat{i}+\hat{j}}{\sqrt{2}} \right) $
$ \therefore $ Resultant $ R=\overrightarrow{OR}+\overrightarrow{OS}+\overrightarrow{OT} $
$=a\left( \frac{\hat{i}+\hat{k}}{\sqrt{2}} \right)+2a\left( \frac{\hat{k}+\hat{i}}{\sqrt{2}} \right)+3a\left( \frac{\hat{i}+\hat{j}}{\sqrt{2}} \right) $
$=\frac{5a}{\sqrt{2}}\hat{i}+\frac{4a}{\sqrt{2}}\hat{j}+\frac{3a}{\sqrt{2}}\hat{k} $
$ \therefore $ $ |R|=\sqrt{\frac{25{{a}^{2}}}{2}+\frac{16{{a}^{2}}}{2}+\frac{9{{a}^{2}}}{2}}=5a $