Q. The values of x satisfying the inequality $| x^{3} -1|\geq 1- x$ belong to
Linear Inequalities
Solution:
$| x^{3} -1|\geq 1- x \Rightarrow | x -1| (x^{2} + x +1) \geq 1- x$
$[\because \: x^{2} + x +1 > 0]$
Let $x < 1$, then we get
$(1- x)(x^{2} + x +1) \geq 1- x$
$ \Rightarrow \: (x -1)(x^{2} + x +1-1) \leq 0$
$ \Rightarrow \:x(x +1)(x -1) \leq 0 $
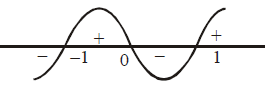
Solving by method of intervals we get
$x \in (- \infty , -1] \cup [0, 1]$
Let $x \geq 1$ , then, we get
$(x -1)(x^{2} + x +1) \geq 1- x$
$\Rightarrow \: (x -1)(x^{2} + x + 2) \geq 0 $
$ \Rightarrow \: x \geq 1 [\because \: x^{2} + x + 2 > 0 \, \forall \, x \, \in \, R]$
$\Rightarrow \: x \, \in [ 1, \infty )$
Combining the two solutions we get
$ x \in ( - \infty , - 1 ]\cup [0, 1] \cup [ 1, \infty )$
or $ x \in ( -\infty , -1] \cup [ 0, \infty)$