Q. The value of $\sin^{-1} \left( \frac{1 }{\sqrt{5}}\right) + \cot^{-1} (3)$ is
VITEEEVITEEE 2016
Solution:
Consider $\sin ^{-1}\left(\frac{1}{\sqrt{5}}\right)+\cot ^{-1} 3 \ldots$ (i)
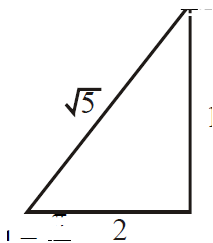
We have, $\sin ^{-1}\left(\frac{1}{\sqrt{5}}\right)=\cot ^{-1} 2$
$\therefore $ From equation (i), we have
$\cot ^{-1} 2+\cot ^{-1} 3=\tan ^{-1} \frac{1}{2}+\tan ^{-1} \frac{1}{3}$
$=\tan ^{-1}\left(\frac{\frac{1}{2}+\frac{1}{3}}{1-\frac{1}{2} \cdot \frac{1}{3}}\right) $
$=\tan ^{-1}\left(\frac{\frac{5}{6}}{\frac{6-1}{6}}\right)=\tan ^{-1} 1=\frac{\pi}{4}$
Hence, $\sin ^{-1}\left(\frac{1}{\sqrt{5}}\right)+\cot ^{-1} 3=\frac{\pi}{4}$