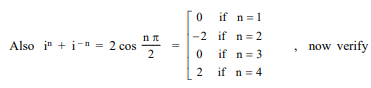Question

The value of $i^n+i^{-n}$, for $i=\sqrt{-1}$ and $n \in I$ is:

• A. $\frac{2^{ n }}{(1- i )^{2 m }}+\frac{(1+ i )^{2 n }}{2^{ n }}$
• B. $\frac{(1+ i )^{2 n }}{2^{ n }}+\frac{(1- i )^{2 n }}{2^{ n }}$
• C. $\frac{(1+i)^{2 n}}{2^{ n }}+\frac{2^{ n }}{(1- i )^{2 n }}$
• D. $\frac{2^{ n }}{(1+i)^{2 n }}+\frac{2^{ n }}{(1-i)^{2 n }}$

Answer 1

Answer: (B), (D)

Note that $\frac{(1+i)^{2 n }}{2^{ n }}=\frac{\left((1+ i )^2\right)^{ n }}{2^{ n }}=\frac{(2 i )^{ n }}{2^{ n }}= i ^{ n } \Rightarrow \frac{2^{ n }}{(1+ i )^{2 n }}= i ^{- n }$
and $\frac{(1-i)^{2 n}}{2^n}=i^{-n} \Rightarrow \frac{2^n}{(1-i)^{2 n}}=i^n$