Q. The torque $\tau$ on a body about a given point is found to be equal to A x L, where A is a constant vector and L is the angular momentum of the body about that point. From this it follows that
IIT JEEIIT JEE 1998System of Particles and Rotational Motion
Solution:
$ (a) \tau =A \times L $
i.e $ \, \, \, \, \, \, \, \, \frac{dL}{dt } =A \times L $
This relation implies that $ \frac{dL}{dt }$is perpendicular to both A and L Therefore, option (a) is correct.
(c) Here, $L L=L^2 $
Differentiating w.r.t. time, we get
$ \, \, \, \, \, \, L . \frac{dL}{dt } + \frac{dL}{dt } .L = 2L \frac{dL}{dt }$
$\Rightarrow \, \, \, \, \, \, \, \, 2 L . \frac{dL}{dt } = 2L \frac{dL}{dt }$
But since, $L- \frac{dL}{dt }$
$\therefore \, \, \, \, \, \, \, \, \, \, \, L . \frac{dL}{dt } =0 $
Therefore, from Eq. (i) $ \frac{dL}{dt } =0$ or magnitude of L i.e. L does not change with time,
(b) So far we are confirm about two points
(1) $ \, \, \, \, \, \, \, \, \, \, \, \, \tau or \frac{dL}{dt} \perp L $ and
(2) | L | = L is not changing with time, therefore, it is a case
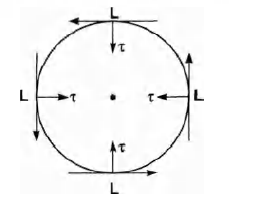
when direction of L is changing but its magnitude is constant and x is perpendicular to L at all points.
This can be written as
If $ L= (acos \theta ) \widehat{i} + (a sin \theta ) \widehat{j}$
Here, a = positive constant
Then, $ \tau = (asin \theta ) \widehat{i}-( a cos \theta )\widehat{j} $
So, that $ L \tau = 0 \, \, and \, \, L \perp \tau $
Now, A is constant vector and it is always perpendicular to x.
Thus, A can be written as A = A $ \widehat{k}$
we can see that L $\bullet$ A = 0 i.e. L$\perp$ A also.
Thus, we can say that component of L along A is zero or component of L along A is always constant.
Finally we conclude that $\tau$, A and L are always mutually perpendicular.