Q.
The top in figure has a moment of inertia of $4.00 \times$ $10^{-4} kg \cdot m ^{2}$ and is initially at rest. It is free to rotate about the stationary axis $A A^{\prime} . A$ string, wrapped around a peg along the axis of the top, is pulled in such a manner as to maintain a constant tension of $2.5 N$. If the string does not slip while it is unwound from the peg, what is the angular speed of the top after $80.0 \,cm$ of string has been pulled off the peg?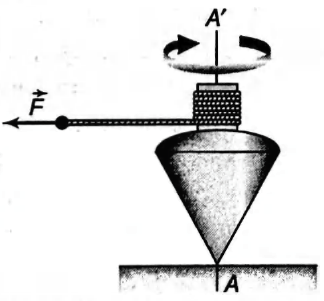
System of Particles and Rotational Motion
Solution: