Q.
The time period of vertical simple harmonic motion of the block shown in the diagram is $T=\frac{x \pi}{y} s$. Find $(x +y)$. Given that the spring is massless and ideal with $k=20\, N / m$, the pulleys are massless and smooth and the block's mass is $m=5 \,kg$, the inclined plane is at $\theta=30^{\circ}$ to the horizontal and the thread is inextensible and massless.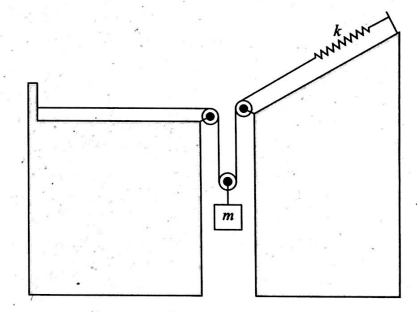
Oscillations
Solution: