Q.
The three rods shown in figure have identical dimensions. Heat flows from the hot end at a rate of $40\, W$ in the arrangement (a). Find the rates of heat flow when the rods are joined as in arrangement (b). (Assume $K_{ Al }=200 \,W / m ^{\circ} C$ and $\left.K_{ cu }=400\, W / m ^{\circ} C \right)$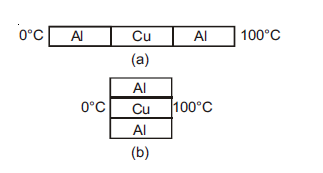
Thermal Properties of Matter
Solution:
