Q.
The temperature of the two outer surfaces of a composite slab, consisting of two materials having coefficients of thermal conductivity $ K $ and $ 2K $ and thickness $ x $ and $ 4x $ , respectively are $ T_2 $ and $ T_1( T_2 > T_1) $ The rate of heat transfer through the slab, in a steady state is $ \left(\frac{A\left(T_{2}-T_{1}\right)K}{x}\right)f $ , with $ f $ equals to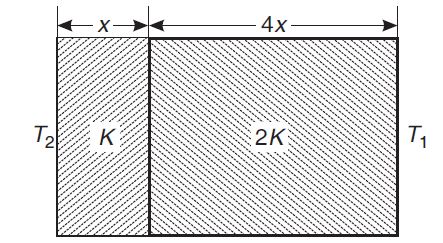
UPSEEUPSEE 2007
Solution: