Question

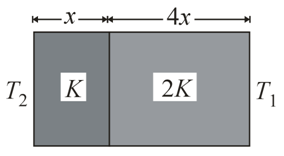
The temperature of the two outer surfaces of a composite slab, consisting of two materials having coefficients of thermal conductivity $k$ and $2K$ and thickness $x$ and $4x$ respectively are $T_{2}$ and $T_{1}\left(T_{2} > T_{1}\right)$ . The rate of heat transfer through the slab, in a steady-state is $\left(\frac{A \left(T_{2} - T_{1}\right) K}{x}\right)f$ with $f$ equal to:-

• A. $1$
• B. $\frac{1}{2}$
• C. $\frac{2}{3}$
• D. $\frac{1}{3}$

Answer 1

Answer: (D)

For slabs in series, we have :
$R_{e q}=R_{1}+R_{2}$
i.e., $\frac{5 x}{K_{e q .} A}=\frac{4 x}{2 K A}+\frac{x}{K A}$
$K_{e q .}=\frac{5 K}{3}$
Now, in steady state, rate of heat transfer through the slab
$=\frac{K_{e q .} A \left(T_{2} - T_{1}\right)}{5 x}=\left(\frac{A \left(T_{2} - T_{1}\right) K}{x}\right)f$
Putting the value of $K_{e q}$ . we get
$f=\frac{1}{3}$