1. Tardigrade
  2. Question
  3. Physics
  4. The temperature-entropy diagram of a reversible engine cycle is given in the figure. Its efficiency is:

Question Error Report

Thank you for reporting, we will resolve it shortly

Back to Question

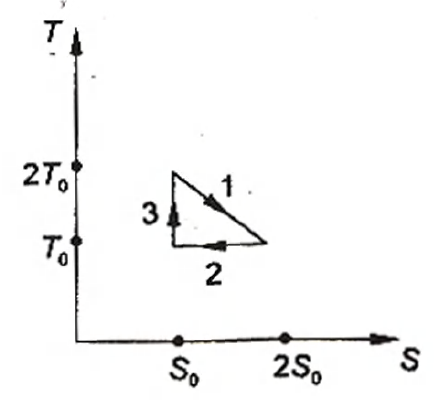
Q. The temperature-entropy diagram of a reversible engine cycle is given in the figure. Its efficiency is: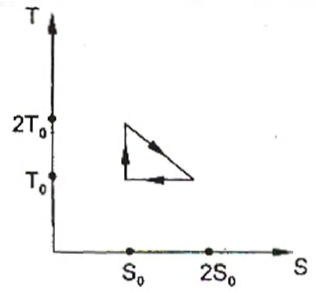Physics Question Image

AIEEEAIEEE 2005Thermodynamics

Solution:

According to the figure
$Q_{1}=T_{0}\,S_{0}+\frac{1}{2} T_{0}\,S_{0}=\frac{3}{2}=T_{0}\,S_{0}$
$Q_{2}=T_{0}\left(2S_{0}-S_{0}\right)=T_{0}\,S_{0}$
$Q_{3}=0$
$\eta=\frac{W}{Q_{1}}=\frac{Q_{1}-Q_{2}}{Q_{1}}$
$=1-\frac{Q_{2}}{Q_{1}}=1-\frac{2}{3}$
$=\frac{1}{3}$

Solution Image