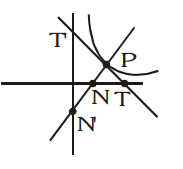
Question

The tangent to the hyperbola $xy = c ^2$ at the point $P$ intersects the $x$-axis at $T$ and the $y$-axis at $T ^{\prime}$. The normal to the hyperbola at $P$ intersects the $x$-axis at $N$ and the y-axis at $N ^{\prime}$. The areas of the triangles PNT and $PN ^{\prime} T ^{\prime}$ are $\Delta$ and $\Delta^{\prime}$ respectively, then $\frac{1}{\Delta}+\frac{1}{\Delta^{\prime}}$ is -

• A. equal to 1
• B. depends on $t$
• C. depends on $c$
• D. equal to 2

Answer 1

Answer: (C)

Let point $P$ be $\left( ct , \frac{ c }{ t }\right)$.
Equation of tangent at $P$ is
$x + yt ^2=2 ct$
$\therefore T$ is $(2 c t, 0) \& T^{\prime}$ is $\left(0, \frac{2 c}{t}\right)$
Now equation of normal at $P$ is
$t ^2 x - y = ct ^3-\frac{ c }{ t }$
$\therefore N \left( ct -\frac{ c }{ t ^3}, 0\right) \& N ^{\prime}\left(0, \frac{ c }{ t }- ct ^3\right)$
$\Delta=\frac{1}{2} \frac{ c }{ t }\left(2 ct - ct +\frac{ c }{ t ^3}\right)=\frac{1}{2} \frac{ c ^2}{ t ^4}\left( t ^4+1\right)$
$\Delta^{\prime}=\frac{1}{2} ct \left(\frac{ c }{ t }+ ct ^3\right)=\frac{1}{2} c ^2\left(1+ t ^4\right)$
$\therefore \frac{1}{\Delta}+\frac{1}{\Delta^{\prime}}=\frac{2}{ c ^2}$.