Question

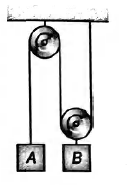
The system shown in the figure consists of a light, inextensible cord, light, frictionless pulleys, and blocks of equal mass. Notice that block B is attached to one of the pulleys. The system is initially held at rest so that the blocks are at the same height above the ground. The blocks are then released. Find the speed of block A at the moment the vertical separation of the blocks is $h.$

• A. $\sqrt{\frac{6gl}{15}}$
• B. $\sqrt{\frac{8gh}{13}}$
• C. $\sqrt{\frac{8gh}{15}}$
• D. $\sqrt{\frac{6gh}{13}}$

Answer 1

Answer: (C)

When block $B$ moves up by $1\, cm$, block $A$ moves down by $2\, cm$ and the separation becomes $3\, cm$.
We then choose the final point to be when $B$ has moved up by $\frac{h}{3}$ and has speed $\frac{v_{A}}{2}$.
Then A has moved down $\frac{2h}{3}$ and has speed $v_{A}:$
$\Delta K+\Delta U=0$
$\left(K_{A}+K_{B}+U_{g}\right)_{f}-\left(K_{A}+K_{B}+U_{g}\right)_{i}=0$
$\left(K_{A}+K_{B}+U_{g}\right)_{i}$
$=\left(K_{A}+K_{B}+U_{g}\right)_{f}$
$0+0+0=\frac{1}{2} m v_{A}^{2}+\frac{1}{2} m\left(\frac{v_{A}}{2}\right)^{2}+\frac{m g h}{3}-\frac{m g 2 h}{3}$
$\frac{m g h}{3}=\frac{5}{8} m v_{A}^{2}$
$\Rightarrow v_{A}=\sqrt{\frac{8 g h}{15}}$