Q.
The speed-time graph of a particle moving along a fixed direction is shown in the figure. The distance traversed by
the particle between $t = 2\,s$ to $t = 6\,s$ is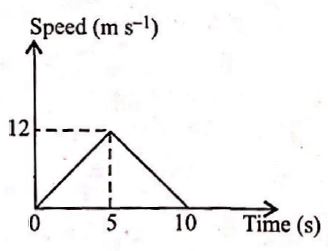
Motion in a Straight Line
Solution:
