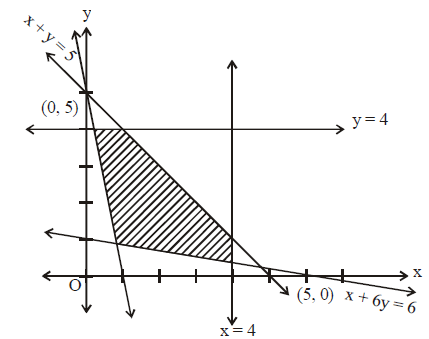
Question

The solution region satisfied by the inequalities x + y $\leq$ 5, x $\leq$ 4, y $\leq$ 4, x $\geq$ 0, y $\geq$ 0,5x + y $\geq$ 5, x + 6y $\geq$ 6, is bounded by

• A. 4 straight lines
• B. 5 straight lines
• C. 6 straight lines
• D. unbounded

Answer 1

Answer: (B)

We find that the solution set satisfies x $\geq$ 0 , y $\geq$ 0 , x $\leq$ 4 , y $\leq$ 4 so that the solution region lies within the square enclosed by the lines x= 0, y = 0, x = 4, y = 4. Moreover, the solution region is bounded by the lines
x + y = 5, …(1)
5x + y = 5 …(2)
x + 6y = 6 …(3)
Line (1) meets the coordinate axes in (5, 0) and (0, 5) and the lines x = 4 and y = 4 in (4, 1) and (1, 4), and 0 < 5 is true.
Hence (0, 0) belongs to the half plane x + y $\leq$ 5. But (0, 0) does not belong to the half planes 5x + y $\leq$ 5 and x + 6y $\leq$6. The line 5x + y = 5, meets the coordinate axes in (1, 0) and (0, 5), and meets the line x = 4 in (4, 1), where as it meets the line y = 4 in (1/5, 4). Similarly x + 6y = 6 meets x = 4 in (4, 1/3) and y = 4 in ( -18, 4).
The solution is marked as the shaded region.