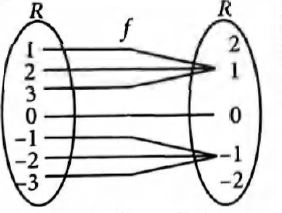
Q.
The signum function, $f$ : $R \to R$ is given by
$f(x) =
\begin{cases}
1, & \text{if } x > 0 \\
0, & \text{if } x=0 \\
-1, & \text{if } x < 0
\end{cases} $ is
Relations and Functions - Part 2
Solution:
We have , $f(1)= f(2)= f(3) = 1$
$f(0 ) = 0$
$f - (1) = f(-2) = f (-3) = - 1$
Hence, function $f$ is not one-one, so signum function is many-one function.