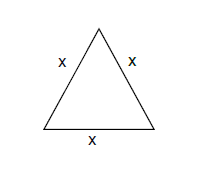Question

The sides of an equilateral triangle are increasing at the rate of 4 cm/sec. The rate at which its area is increasing, when the side is 14 cm.

• A. 42 $cm^2 / \sec$
• B. $ 10\sqrt{3} cm^2 / \sec$
• C. 14 $cm^2 / \sec$
• D. $ 14 \sqrt{3} cm^2 / \sec$

Answer 1

Answer: (B)

Let $x$ be the side of an equilateral triangle and $A$ be the area.
$
\therefore A =\frac{\sqrt{3}}{4} x ^{2}
$
On differentiating both sides with respect to $t$, we get
$
\frac{ dA }{ dt }=\frac{\sqrt{3}}{4} 2 x \frac{ dx }{ dt }
$
Given, $x=10 cm$
and $\frac{d x}{d t}=2 cm / s$
$
\therefore \frac{ dA }{ dt }=\frac{\sqrt{3}}{4} 2 \times(10) \times 2
$
$
=10 \sqrt{3} cm ^{2} / s
$