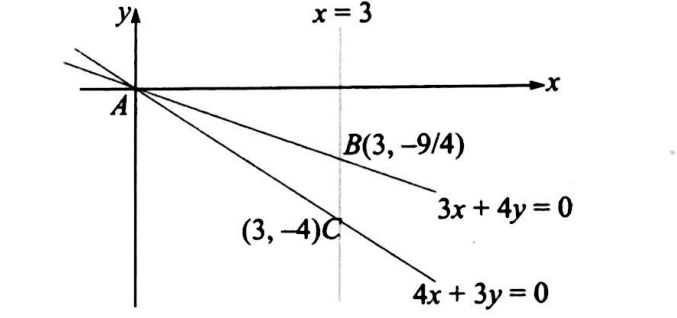
Question

The sides of a triangle $A B C$ lie on the lines $3 x+4 y=0$, $4 x+3 y=0$, and $x=3$. Let $(h, k)$ be the center of the circle inscribed in $\triangle A B C$. The value of $(h+k)$ equals.

Answer 1

The equation of the angle bisector of angle $A$ is
$\frac{3 x+4 y}{5}=\pm \frac{4 x+3 y}{5} \text { or } x=\pm y$

The equation of internal bisector is $x=-y$ Since $h$ and $k$ lie on the line $x=-y$, we have
$h+k=0$