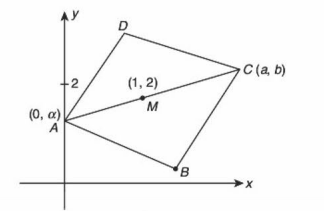
Question

The sides of a rhombus $ABCD$ are parallel to the lines, $x - y + 2 = 0$ and $7x - y + 3 = 0$. If the diagonals of the rhombus intersect at $P(1, 2)$ and the vertex $A$ (different from the origin) is on the $y-$ axis, then the ordinate of $A$ is :

• A. $\frac{5}{2}$
• B. $\frac{7}{4}$
• C. 2
• D. $\frac{7}{2}$

Answer 1

Answer: (A)

From the given data, we plot the graph below.

Now, midpoint of $AC$ is
$\frac{a+0}{2}=1 \Rightarrow a=2$
$\frac{b+\alpha}{2}=2 \Rightarrow b+\alpha=4$
Sides of rhombus are parallel to the lines $x-y+2=0$ and $7 x-y+3=0$.
Equation of parallel lines to diagonals
$\frac{x-y+2}{\sqrt{2}} \pm \frac{7 x-y+3}{5 \sqrt{2}} \Rightarrow 2 x+4 y-7=0$ and $12 x-6 y+13=0$
So, slope $=\frac{-1}{2}$ and $2=$ slope of $A C$
Therefore, $\frac{2-\alpha}{1-0}=\frac{-1}{2}$ or $2 \Rightarrow 2-\alpha=-\frac{1}{2}$ or $2 \Rightarrow \alpha=\frac{5}{2}$ or 0
Therefore, ordinate of $A$ is $\frac{5}{2}$.