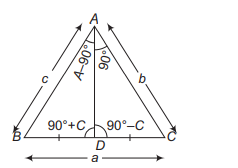
Question

The sides $B C, C A$ and $A B$ of a $\triangle A B C$ are of lengths $a, b$, and $c$ respectively. If $D$ is the mid-point of $B C$ and $A D$ is perpendicular to $A C$, then the value of $\cos A \cos C$ is

• A. $\frac{3\left(a^2-c^2\right)}{2 a c}$
• B. $\frac{3\left(a^2-c^2\right)}{3 b c}$
• C. $\frac{\left(a^2-c^2\right)}{3 a c}$
• D. $\frac{2\left(c^2-a^2\right)}{3 a c}$

Answer 1

Answer: (D)

Using sine rule in $\triangle A C D$,
$ \frac{\sin \left(90^{\circ}-C\right)}{b}=\frac{\sin 90^{\circ}}{\frac{a}{2}}$
$\Rightarrow \cos C=\frac{2 b}{a} $
and in $ \Delta A B D,$
$ \frac{\sin \left(A-90^{\circ}\right)}{\frac{a}{2}}=\frac{\sin \left(90^{\circ}+C\right)}{c}$
$\Rightarrow-\frac{\cos A}{\frac{a}{2}}=\frac{\cos C}{c} \Rightarrow \cos A=-\frac{b}{c}$
$\Rightarrow \frac{b^2+c^2-a^2}{2 b c}=-\frac{b}{c} \Rightarrow c^2-a^2=-3 b^2$
$\therefore \cos A \cos C=-\frac{2 b^2}{a c}=\frac{2}{3 a c}\left(c^2-a^2\right)$