Question

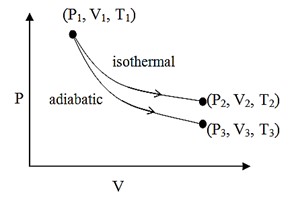
The reversible expansion of an ideal gas under adiabatic and isothermal conditions is shown in the figure. Which of the following statement is incorrect?

• A. $T_{3}>T_{1}$
• B. $T_{1}=T_{2}$
• C. $\Delta U_{\text{isothermal}}>\Delta U_{\text{adiabatic}}$
• D. $W_{\text{isothermal}}>w_{\text{adiabatic}}$

Answer 1

Answer: (A)

Use ideal gas equation $PV=nRT$ and consider,
Work done=area under P−V curve.
Step 1: Calculate the relation between $T_{1 , }T_{2}andT_{3}$ ​ Since temperature is constant in any isothermal process, $T_{1}=T_{2}$ . From ideal gas equation $T_{2}=\frac{P_{2} V_{2}}{nR}andT_{3}=\frac{P_{3} V_{3}}{nR}$ ​
​ From the graph we can see $P_{2}>P_{3}$ and $T_{2}>T_{3}$ ​
So, relation between temperatures is: $T_{1}=T_{2}>T_{3}$ ​
Step 2: Compare the work done between the two processes. The work done is the area under the P−V curve. Since the isothermal curve is above the adiabatic curve at all times, the area under the isothermal curve is greater.
$\Longrightarrow W$ isothermal $> W$ adiabatic
Step 3: Calculate $\Delta U$ for both the processes.
We know that $\Delta U = nC _{ V } \Delta T$
$\Longrightarrow \Delta U$ isothermal $= nC _{ V }\left( T _{2}- T _{1}\right)=0 \quad$ (since, $\left.T _{1}= T _{2}\right)$
and for adiabatic process we have
$\Longrightarrow \Delta U$ adiabatic $={ }^{n} C_{V}\left(T_{3}-T_{1}\right)<0,\left(\right.$ Since $\left.T_{1}>T_{3}\right)$
Thus, $\Delta U$ isothermal $>\Delta U$ adiabatic