Q.
The region between two concentric spheres of radii $'a'$ and $'b'$, respectively (see figure), has volume charge density $\rho = \frac{A}{r}$, where $A$ is a constant and $r$ is the distance from the centre. At the centre of the spheres is a point charge $Q$. The value of $A$ such that the electric field in the region between the spheres will be constant, is :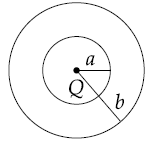
Solution:
