1. Tardigrade
  2. Question
  3. Physics
  4. The region between the parallel plates of a capacitor is filled with parallel layers of air and paper (of dielectric constant 4). The space between the plates is 1 mm and the thickness of paper is 0.75 mm. The ratio of the voltages across air and paper is

Question Error Report

Thank you for reporting, we will resolve it shortly

Back to Question

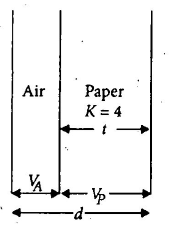
Q. The region between the parallel plates of a capacitor is filled with parallel layers of air and paper (of dielectric constant $4$). The space between the plates is $1 \,mm$ and the thickness of paper is $0.75\, mm$. The ratio of the voltages across air and paper is

COMEDKCOMEDK 2014Electrostatic Potential and Capacitance

Solution:

Here, $d = 1 \, mm, t = 0.75\, mm$
The given capacitor is equivalent to a two capacitors are connected in series. As in series charge on each capacitor is same,
$ \therefore \, Q_A = Q_P$
where the subscripts A and P refer air and paper respectively,
Thus,
$C_{A} V_{A} = C_{P} V_{P} $
$ \frac{V_{A}}{V_{P}} = \frac{C_{P}}{C_{A}} = \frac{\frac{e_{0}KA}{t}}{\frac{e_{0}A}{\left(d-t\right)}} = \frac{K\left(d-t\right)}{t} $
$ = \frac{4\left(0.25 mm\right)}{0.75 mm} = \frac{4}{3}$

Solution Image