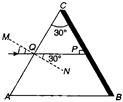
Q. The refractive index of the material of a prism is $ \sqrt{2} $ and its refracting angle is $ 30^{\circ} $ . One of the refracting surfaces of the prism is made a mirror inwards. A beam of monochromatic light entering the prism from the other face will retrace its path after reflection from the mirrored surface, if its angle of incidence on the prism is:
Delhi UMET/DPMTDelhi UMET/DPMT 2006
Solution:
According to the given condition, the beam light will retrace its path after reflection from $BC$
$ \angle CPQ={{90}^{\circ}} $ Thus, angle of refraction at surface $AC$
$ \angle PQN=\angle r={{90}^{\circ}}-{{60}^{\circ}}={{30}^{\circ}} $
By Snells law $ \mu =\frac{\sin i}{\sin r} $
$ \Rightarrow $ $ \sqrt{2}=\frac{\sin i}{\sin {{30}^{\circ}}} $
$ \therefore $ $ \sqrt{2}\times \sin {{30}^{\circ}}=\sin i $
$ \Rightarrow $ $ \sqrt{2}\times \frac{1}{2}=\sin i $
$ \Rightarrow $ $ i={{45}^{\circ}} $