Q.
The radius of the sphere
$x^{2} + y^{2} + z^{2 }= 49, \,2x + 3y -z - 5\sqrt{14} = 0$ is
VITEEEVITEEE 2018
Solution:
The sphere $x^2 + y^2 + z^2 = 49$
has centre at the origin (0, 0, 0) and radius 7.
Disance of the plane
$2x + 3y-z-5-\sqrt{14} = 0$
from the origin
$= \frac{\left|2\left(0\right) + 3\left(0\right)-\left(0\right)-5\sqrt{14}\right|}{\sqrt{2^{2}+3^{2}+\left(-1\right)^{2}}}$
$= \frac{\left|-5\sqrt{14}\right|}{\sqrt{14}} = \frac{-5\sqrt{14}}{\sqrt{14}} = 5$
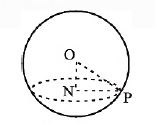
Thus in Figure; $OP = 7, \,ON = 5$
$NP^{2} = OP^{2} - ON^{2} = \left(7\right)^{2} - \left(5\right)^{2}$
$= 49-25=24
\therefore \quad NP = 2\sqrt{6 }$ Hence the radius of the circle
$= NP = 2\sqrt{6 }$